Math Fest 2008
The Brachistochrone Revisited: A Timely Consideration
Thursday, July 31, 2008
|
|
Abstract:
In June 1696 Johann Bernoulli published as a challenge
the following problem. "Given two points
A and B in a vertical plane, what is the curve traced out by a point acted
on only by gravity, which starts at A and reaches B in the shortest time."
This challenge, the brachistochrone, is one
the origins of the Calculus of Variations. The problem is to determine
for a frictionless bead accelerated from rest the path that would minimize
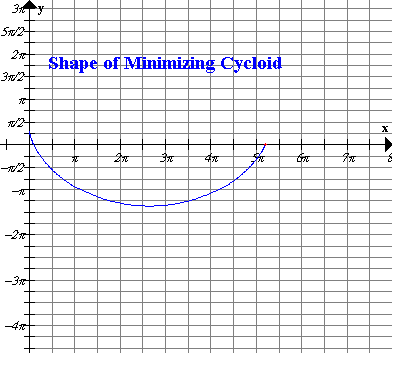
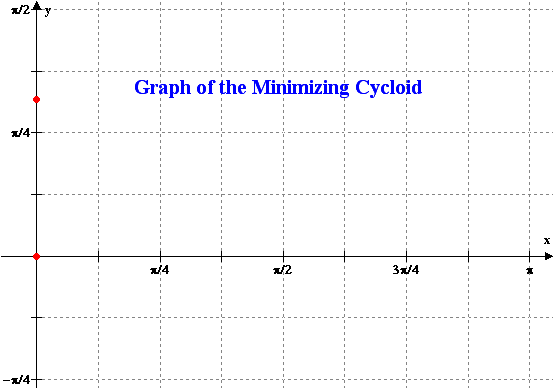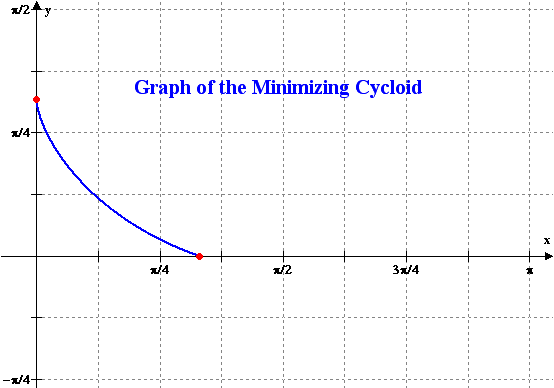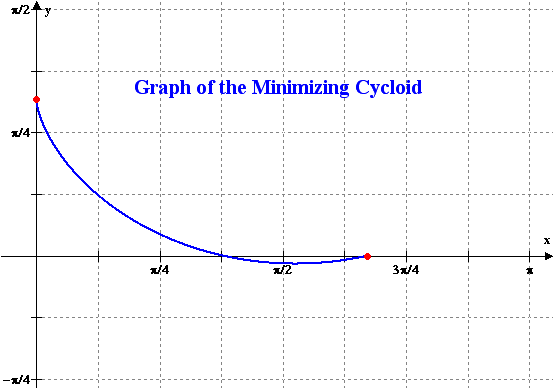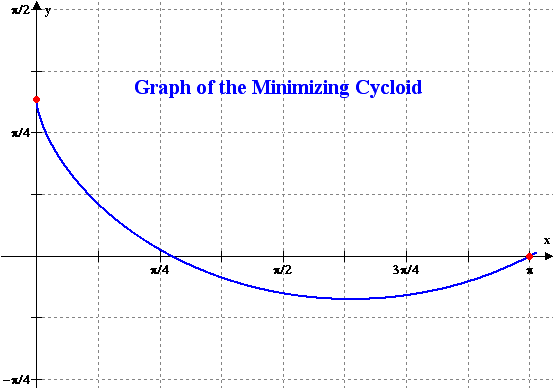
the time of descent between two specified points. The well-known solution
is an inverted cycloid. The fundamental independent variable of the
problem is r, the ratio of the horizontal to
vertical displacement between the two points. Properties of the cycloid
solution as r varies, including its uniqueness,
are elaborated. In particular, if r exceeds ![]() , then the least time path attains an absolute minimum
below the terminal point of the trajectory.
, then the least time path attains an absolute minimum
below the terminal point of the trajectory.
In this presentation explicit asymptotic expansions for the time of
descent for both large and small r are developed.
Relatively simple and computationally efficient formulas that allow
for an accurate graph of the minimizing cycloid for any value of r
are derived. In addition, variational calculations that minimize the
time of descent for trial function trajectories are presented. The first
trajectories considered were piecewise linear segments. Their ability
to approximate the solution of the brachistochrone is summarized.
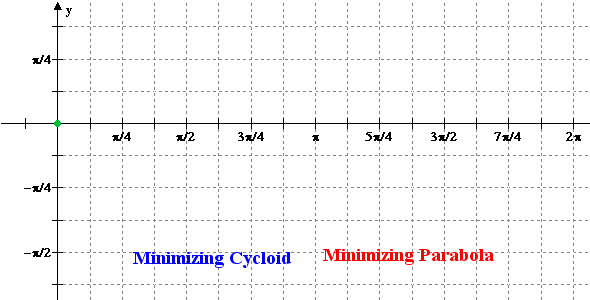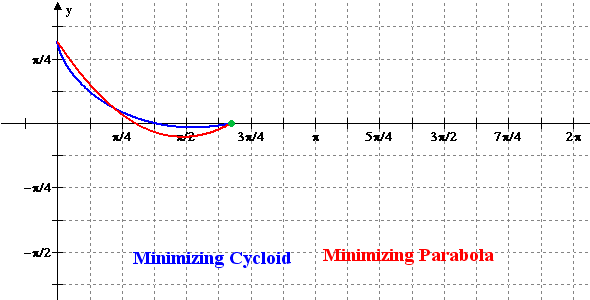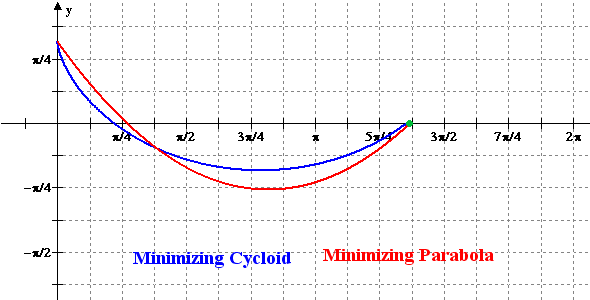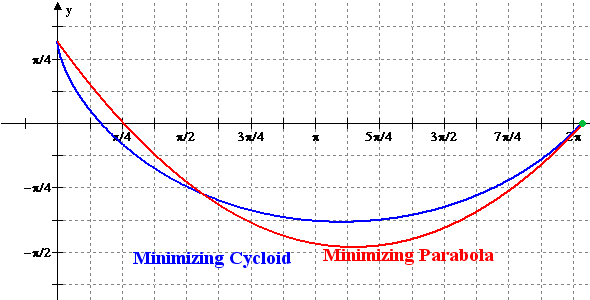
Finally, a rather thorough analysis of a minimizing parabola is given.
Despite the fact that having y descend as a quadratic function
of x between the two points leaves only one free parameter, such
a trajectory is able to come very close in matching the time of descent
of the minimizing cycloid.
|
Figure 2: Animation of the Minimizing Cycloid
and the Minimizing Parabola versus x = r
|
Figure 3: Animation of the
Minimizing Cycloid and the Variational Solutions versus x =
r |
|
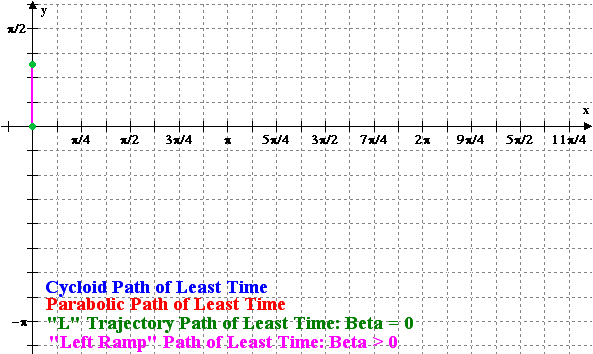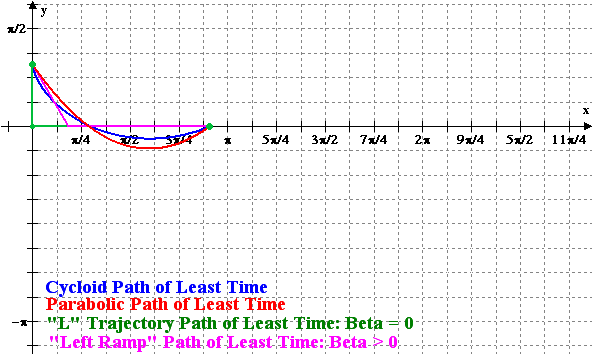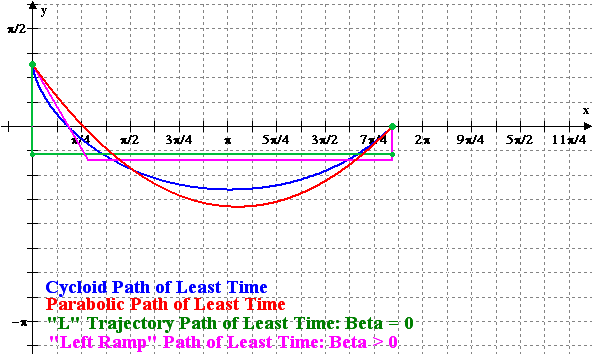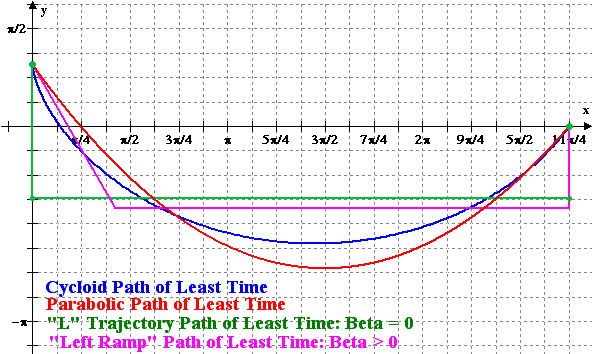
|
A comparison of the total time of travel between the different variational methods and the minimizing cycloid is displayed in Figure 4. The notation is that T(1, r, 0, r) is the straight line trajectory, T(gamma1(r), 0, 0, r) is the “L” trajectory and T(gamma2(r), 0, 0, r) is the “Left Ramp” trajectory. For the least-time parabolic trajectory the discrete points represent the approximate solutions obtained by Newton’s method.
Figure 4
A summary with results is available at https://drive.google.com/file/d/18VppQoujSM2x3sQEKTC4715URgmiXemx/view?usp=drive_link .
A more detailed version with derivations
is https://drive.google.com/file/d/1Dkz9Se_cGBl2Pf8MbG8s7hQIaySCrqyr/view?usp=drive_link
.