Calculus Winplot Files
The following Winplot files can be downloaded. Winplot itself can be downloaded
at https://drive.google.com/file/d/1Nc9lX0DwB4_nbsFnQaDtWwY9EAEuenqq/view?usp=sharing.
An online
tutorial is also available. To download a one of the files shown
below, left click with the mouse and save the file to your
local disk. A sample output is shown in the graphic above.
Calculus I Examples
Tangent Line
to a Circle: Animate on p to Change the Point P, Animate on a
to Change the Radius, Animate on h , k to Change the
Center.
Geometric
Construction of the Tangent Line to a Parabola: Animate on
a to Change the Point P, Animate on d to Change
the Directrix.
Illustration
of Defining a Piece-Wise Function
Illustration of
a Limit: Animate on a (the Fixed x Value),
e (Epsilon), and p (Varies x) for a
Given User Defined Function g(x)
A Second
(better!) Illustration of a Limit Authored by John Ganci: Animate
on a (the Fixed x Value), e (Epsilon), and d
(Delta) for a User Defined Function FF(x). The parameter p
varies x near a.
Illustration
of Problem 19 of Project 1 Animate on a to Change its Value
Calculating
the Instantaneous Velocity of a Falling Object Animate
on p to Change the Time, Animate on s to Change
Delta Time
The Derivative
as the Slope of the Tangent Line: Animate on a to
Change the Point on the User Defined Function g(x),
Animate on h to change Delta x
Illustration
of Problem 1 of Project 2. Animate on a to Change
the Point Where the Tangent Line Touches the Curve y
= abs( 4 - x^2)
The Central
Difference Approximation to the Derivative: Animate on a
to Change the Point on the User Defined Function g(x),
Animate on h to change Delta x
Project 3 Problem
1 : Animate on a to move the point on both of y = f(x)
and x = f(y)
Mean Value
Theorem Illustrated on Project 3 Problem 4a : Animate on A and B to Move
the Secant Line
Illustration
of the Linear and Quadatic Approximation about a Point on
a Curve. Project 3 Problem 6
Illustration
of a Cylinder Inscribed in a Sphere (Project 4, Problem
12). This is a Three-Dimensional Plot which Needs to Opened in
the 3-dim Window. Vary the Parameter b to Change the Cylinder.
Torus Made by Revolving
a Circle of Radius 1 Centered at (0,2) About the x
Axis
Torus Made by Revolving
a Circle of Radius 1 Centered at (0,2) About the x
Axis with an Inscribed Sphere (Volume of Revolution About y
Axis!)
A nice view of a Torus:
File Generated by John Ganci:
Surface Area
of a Sphere Calculated Using a Chord Length
Illustration
of the Archimedian Property of a Sphere
Proof of the
Archimedian Property of a Sphere
Calculus II Examples
Illustration
of Slope of Tangent Line to y = 4xln(1
- 2/x)
Illustration of
Slope Fields for the Derivative equal to a Piecewise Function
(Project 3 Problem 6.d)
Graph of
Lissajous figures (a is the horizontal amplitude, b is vertical
amplitude, f is the frequency ratio of the vertical oscillator
to the horizontal oscillator)
Graph of the Trochoid
(a is the "wheel" radius, b is distance from the center of
the "wheel", p is the "time" parameter)
Graph of the Cycloid
(a is the "wheel radius", p is the "time" parameter)
Graph of the
"Bi-Cycloid (a is the "wheel radius", p is the "time" parameter)
Parameterizing
the Unit Hyperbola using sinh and cosh (a is the parameter on
the unit circle)
Graph of the
Astroid and its Tangent Line as in Problem 3 of Project 6 (a is the Dimension
of the Astroid, p is the "angle" parameter)
Graph of the Epicycloid
(a is the inner circle radius, b is the rotating circle radius,
p is the "time" parameter)
Graph of
both the Epicycloid and the Hypocycloid (a is the inner circle radius, b
is the rotating circle radius, p is the "time" parameter)
Graph of the
"Golden Spiral" showing the limit point as the number of sprials
goes to infinity
Three-D
Graph of the Intersection of a Cone with a Plane (k is the Cone
Angle, Plane is z = a*x + b*y +c )
Graph of the
Quadratic Equation x^2/a+y^2/b = 1
Illustration
of the Definition of a Parabola: Focus at (0, p), Directrix y
= - p
Second Illustration
of the Definition of a specific Parabola: y^2 - 8x
- 4y = 20 : Focus at (-1, 2), Directrix x = - 5
Graph of the Ellipse
x^2/a^2+y^2/b^2 = 1 ( k is the Eccentricity, b = a*sqrt(1-k^2),
p Moves the Point on the Ellipse )
Graph
of the Ellipse (x-2)^2/9+(y+5)^2/4 = 1 Showing the PF = eccentricity*PD
property, p Moves the Point on the Ellipse.
Graph of the
Ellipse (x-2)^2/9+(y+5)^2/4 = 1 Showing the reflective property
of the two focal points, p Moves the Point on the Ellipse.
Graph of
the Hyperbola (y+1)^2/9-(x-3)^2/36 = 1 Showing the PF = eccentricity*PD
property, p Moves two Points on the Hyperbola.
Graph of the
Hyperbola x^2/a^2 - y^2/b^2 = 1 ( k is the Eccentricity, b = a*sqrt(k^2-1),
p Moves Points on the Hyperbola)
Graph of a General
Conic Section: ( e is the Eccentricity, k = Distance from Focus
to Diretrix, s varies Orientation of Directrix)
Illustration of the
"Four Bugs Problem" from Group Project 4: Animate on p to
Move the Four Bugs
Illustration of
Vector Addition in 2D: a is the Length of Vector 1,
p is its Angle, b is the Length of Vector 2, c is its Angle
Illustration
in 2D of Projecting a Vector A (RED) onto a Vector B (BLUE):
a is the Length of Vector A, p is its Angle, b is the Length
of Vector B, c is its Angle
Illustration of
a Vector in 3D: a is the Length of the Vector, p is
its Polar Angle and c is its Azimuth
Illustration
of Vector Addition in 3D: a is the Length of Vector 1, p is its Polar
Angle and c is its Azimuth, b is the Length of Vector 2, with Angles u and
v
Illustration
of the Geometric Definition of the Vector Cross Product:
< a, b, c> is the BLUE vector A; < e, f, g> is the RED vector
B; the PURPLE vector is the projection of B into the plane perpendicular
to A at the base of A; the GREEN vector is the rotation of the projected vector
90 degrees CCW about the pole of A; the BLACK vector is the CROSS of A with
B.
Illustration
of the Vector Cross Product: a is the Length of Vector
1 (BLUE), p is its Polar Angle and c is its Azimuth, b is the
Length of Vector 2 (RED), with Angles u and v
An
Elliptic Hyperboloid with Axis Along the z Axis:
Animate on a to Change from a one-sheet to a two-sheet Hyperboloid,
Animate on b to Vary Cross Sections at Fixed y , Animate
on c to Vary Cross Sections at Fixed x , Animate
on d to Vary Cross Sections at Fixed z
An
Elliptic Hyperboloid with Axis Along the y Axis:
Animate on a to Change from a one-sheet to a two-sheet Hyperboloid,
Animate on b to Vary Cross Sections at Fixed y , Animate
on c to Vary Cross Sections at Fixed x , Animate
on d to Vary Cross Sections at Fixed z
An
Elliptic Hyperboloid with Axis Along the x Axis:
Animate on a to Change from a one-sheet to a two-sheet Hyperboloid,
Animate on b to Vary Cross Sections at Fixed y , Animate
on c to Vary Cross Sections at Fixed x , Animate
on d to Vary Cross Sections at Fixed z
A
Hyperbolic Paraboloid (Saddle) with Axis Along the z
Axis: Animate on b to Vary Cross Sections at Fixed y
, Animate on c to Vary Cross Sections at Fixed x
, Animate on d to Vary Cross Sections at Fixed z
A
Hyperbolic Paraboloid (Saddle) with Axis Along the y
Axis: Animate on b to Vary Cross Sections at Fixed y
, Animate on c to Vary Cross Sections at Fixed x
, Animate on d to Vary Cross Sections at Fixed z
A
Hyperbolic Paraboloid (Saddle) with Axis Along the x
Axis: Animate on b to Vary Cross Sections at Fixed y
, Animate on c to Vary Cross Sections at Fixed x
, Animate on d to Vary Cross Sections at Fixed z
Calculus III Examples
Illustration
of the Equation of a Plane: Ax + By + Cz
= D, the Normal, < A, B, C
>, and a Parametric Equation of the Line Through the Point
(p, q, s) Normal to the Plane (see Project
1 , Problem 5)
Cylindrical
Coordinates Showing the Unit Vectors r Hat, Theta
Hat and k hat (Animate on E (Theta) and F (z) )
Spherical
Coordinates Showing the Unit Vectors Rho Hat, Phi Hat and
Theta Hat (Animate on E (Theta) and F (Phi) )
Demonstation
that the Intersection of a Plane and a Right Circular Cylinder
is an Ellipse (Animate on D to change radius, a and b to rotate plane)
Motion with Constant
Angular Velocity = w (Animate on w) The Position, Velocity
and Acceleration Vectors are Illustrated: Circular Motion
Motion with Constant
Angular Velocity = w (Animate on w) The Position, Velocity
and Acceleration Vectors are Illustrated: r = 3cos(2theta)
The Evolute
of the Parabola y = x^2 : Animate on Parameter
P to Move on the Parabola and Move the osculating Circle
The Evolute
of the Parabola y = bx^2 : Animate on Parameter P to Move on
the Parabola and Move the osculating Circle
Unit Tangent and
Normal Vectors for a Curve in the x-y plane.
The osculating Circle is also Displayed: Curve 1: A Circle.
Animate on the Parameter P
Unit Tangent and
Normal Vectors for a Curve in the x-y plane.
The osculating Circle is also Displayed: Curve 2: A Parabola.
Animate on the Parameter P
Unit Tangent and
Normal Vectors for a Curve in the x-y plane.
The osculating Circle is also Displayed: Curve 3: A Sine Wave.
Animate on the Parameter P
Unit Tangent
and Normal Vectors for y = sin(x) . The Osculating
Circle and the Evolute are both Displayed. Animate on the Parameter
P
Unit Tangent
and Normal Vectors for y = Acos(bx)
. The Position Vector, the Unit Tangent Vector, the Unit Normal Vector
and the Osculating Circle are all Displayed. Animate on the Parameters
P, A and b
Unit Tangent
and Normal Vectors for y = Asin(bx) .
The Position Vector, the Unit Tangent Vector, the Unit Normal Vector
and the Osculating Circle are all Displayed. Animate on the Parameters
P, A and b
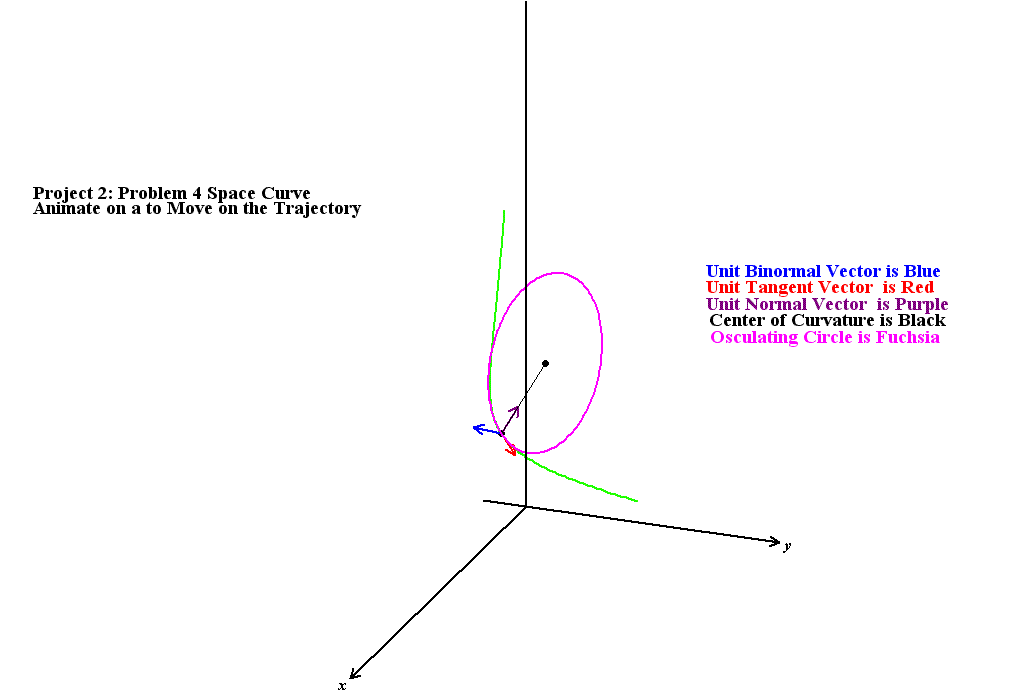
TNB Vectors for
Problem 4 on Project 2. Animate on the Parameter P
A Second View
of the TNB Vectors for Problem 4 on Project 2 Showing the Osculating Circle.
Animate on the Parameter A
TNB Vectors for a Circular
Helix
Example of Using
Unit Vectors to Solve for Angular Acceleration in Dynamics
Illustration of the
Motion in Group Project 1, Problem 1 : Animate on A (time)
Illustration of the
Motion in Group Project 1, Problem 4 (The Ant) : Animate on
P (to see the ant move counter clockwise up the parabola)
Example
of a Tangent Plane and Normal to the surface z =
f(x, y) = 3x^2y + x^3
Example of
a Tangent Plane and Normal to the Sphere z = f(x,
y) = sqrt(16-x^2- y^2)
Example of
a Tangent Plane and Normal to a surface z = f(x,
y) = exp(-x^2-y^2)
Example of
a Tangent Plane and Normal to a surface z = f(x,
y) = x^2 + 2x + y^2 - 6y
Example of
a Tangent Plane and Normal to a surface z = f(x,
y) = xsin(xy)
Project 3 Problem
5 on the Electric Field in a Metal Animate on a (Lamda),
b (Omega), F (E nought), u , v
to vary a "point" on the surface
Project 3 Problem
8 on the Intersection of a Sphere with a Saddle
Project 3 Problem
10 on the Maximum/Minimum on a Closed Region
Fall 2007 Exam
2: Illustation of Finding Max/Min of f(x, y)
= -2xy^3 on a circle of radius a
Group Project
2 Problem 3 on the Steepest Ascent of the Droid on the Glacier
Group Project 2
Problem 4 on the Tangent Plane to a Cone
Group Project 2
Problem 4 on the Tangent Plane to a Curve z = y
f(y/x) for f(x) = 3x
Group Project 2
Problem 4 on the Tangent Plane to a Curve z = y
f(y/x) for f(x) = sin(x)
An
Illustration of Integrating under the Plane x + y
+ 2z = 6 in the First Octant in the Order (Inside to Outside)
z, y, x : Animate on (a, b, c) for (x,
y, z)
An
Illustration of Integrating under the Plane x + y
+ 2z = 6 in the First Octant in the Order (Inside to Outside)
y, z, x : Animate on (a, b, c) for (x,
y, z)
An
Illustration of Integrating under the Plane x + y
+ 2z = 6 in the First Octant in the Order (Inside to Outside)
z, x, y : Animate on (a, b, c) for (x,
y, z)
An
Illustration of Integrating under the Plane x + y
+ 2z = 6 in the First Octant in the Order (Inside to Outside)
x, z, y : Animate on (a, b, c) for (x,
y, z)
An
Illustration of Integrating under the Plane x + y
+ 2z = 6 in the First Octant in the Order (Inside to Outside)
y, x, z : Animate on (a, b, c) for (x,
y, z)
An
Illustration of Integrating under the Plane x + y
+ 2z = 6 in the First Octant in the Order (Inside to Outside)
x, y, z : Animate on (a, b, c) for (x,
y, z)
Project 4 Problem
1e on the Integral of xy over the Region Bounded by
the Coordinate Planes and the Plane 2x + y + 3z
= 6
Project 4 Problem
1f on the Integral of xy over the Region Bounded by
the Coordinate Planes, the Cylinder r = 2 and the Plane
x + z = 3
Project 4 Problem
2b Showing the Three Dimensional Region: 0 < z <
pi - x^2 ; 0 < y < x ; 0 < x
< sqrt (pi)
Project 4 Problem
7b Showing the Three Dimensional Region defined as "Crystal":
Animate on a and b to Vary Over the Domain
Project 4 Problem
7c Showing the Three Dimensional Region in the First Octant
between the two Planes: x + y + z = 1 and
2x + 2y + z = 2
An
Illustration of the Element of Volume in Cylindrical Coordinates:
dV = r d(r) d(theta) d(z) : Animate on the Parameters
Listed in the File
An Illustration
of the Element of Volume in Spherical Coordinates: dV
= rho^2 sin(phi) d(rho) d(phi) d(theta) : Animate on the
Parameters Listed in the File
The Intersection
of a Sphere of Radius a and the Half Space z >
b : r on the "outside", z on the "inside"
: Animate on the Parameters Listed in the File
The Intersection
of a Sphere of Radius a and the Half Space z >
b : z on the "outside", r on the "inside"
: Animate on the Parameters Listed in the File
The Intersection
of a Sphere of Radius a and the Half Space z >
b : Spherical Coordinates : Animate on the Parameters Listed
in the File
A cored
Sphere: The Intersection of a Sphere of Radius a and the
Cylinder r = b : r on the "outside", z
on the "inside" : Animate on the Parameters Listed
A Cylinder
Inscribed Inside of a Sphere with the Height of the Cylinder
as a Variable Parameter
The Sphere Game:
Group Project Problem 3
Miscellaneous Examples
Transformation
of a Rectangle into a Square of Equal Area. The parameter
p (range of zero to one) controls the movement of the "cut"
pieces while the parameters a and b are the dimensions of the
rectangle. Only values of b > a should be used.
Torus with
axis along x: Animate on a to change the mean radius of
the torus about the axis, animate on b to change the "tube" radius,
animate on c to move along the axis
Torus with
axis along z: Animate on a to change the mean radius of
the torus about the axis, animate on b to change the "tube" radius,
animate on c to move along the axis
Torus with
axis along y: Animate on a to change the mean radius of
the torus about the axis, animate on b to change the "tube" radius,
animate on c to move along the axis
Double Torus:
Animate on a to change the mean radius of the torus about the
axis, animate on b to change the "tube" radius
Triple Torus:
Animate on a to change the mean radius of the torus about the
axis, animate on b to change the "tube" radius
Two Toruses
(wheels) with an axle: animate on D to spin the wheels
Four
Toruses (wheels) with a axles: animate on D to spin the wheels
Stereographic_Projection_z_and_theta_input
Animate on S and O to move the source point
Stereographic_Projection_to
Z and 1/Z_z and_theta_input Animate on S and O to move the source point
Projection
of a Circle on Unit Sphere to a Circle in C Animate on O to rotate
the source point
Projection
of a Circle in C onto a Circle on Unit Sphere Animate on O to rotate
the source point
Projection
of a Polar Circle on Unit Sphere to a Line in C Animate on O to rotate
the source point
Projection
of a Line (Cartesian Input) in C to a Polar Circle on Unit Sphere Animate
on P to move the source point
Projection
of a Line (Polar Input) in C to a Polar Circle on Unit Sphere Animate on
P to move the source point
Construction
of the Centroid of a Triangle as the Intersection of the Medians: Vertices
at (0,0), (a,b), (c,0). Animate on a, b and c
Construction
of the In Center of a Triangle as the Intersection of the Angle Bisectors:
Sides of length a, b and c. Animate on a, b and c
Construction
of the Circum Center of a Triangle as the Intersection of the Perpendicular
Bisectors of the Sides: Vertices at (0,0), (a,b), (c,0).
Animate on a, b and c
Construction
of the Ortho Center of a Triangle as the Intersection of the Altitudes: Vertices
at (0,0), (a,b), (c,0). Animate on a, b and c
Home

